2x6 Wood Beam Span Calculator - Deflection and Load Analysis

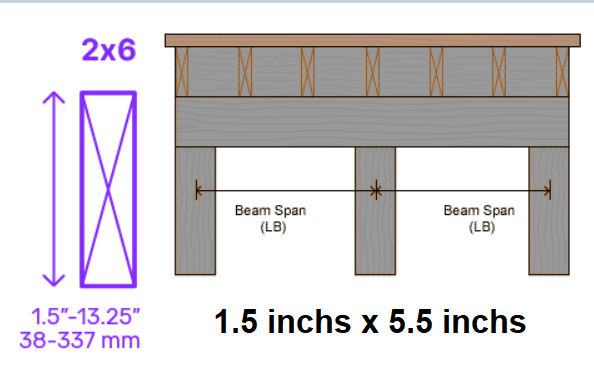
2x6 Wood Beam Overview

2x6 Wood Beam is a versatile and commonly used lumber size for various construction and DIY projects. Below are its key details:

• Nominal Size: 2 inches × 6 inches
• Actual Size: Typically 1.5 inches × 5.5 inches (38mm × 140mm)
• Materials: Made from softwood (e.g., pine, cedar) or hardwood (e.g., oak, maple).


• Applications:
  
  • Wall framing and studs
  • Decking and fence rails
  • Roof framing and light structural supports
  • Furniture and shelving projects


• Advantages: Lightweight, easy to work with, and suitable for a range of projects.


• Limitations: Limited load-bearing capacity for larger or heavy-duty structures.

2x6 wood beams are a practical choice for many small to medium construction projects due to their balance of strength, size, and ease of handling.

Deflection of a Wood Beam Formula

To calculate the deflection of a wood beam with a rectangular cross-section, use the following formula:

Where:

\(\delta\) (Deflection):

The deflection at the midspan of the wood beam in inches.

\(w\) (Uniform Load):

The uniformly distributed linear load applied to the beam, in pound-force per inch (lbf/in).

\(L\) (Beam Span):

The span or unbraced length of the beam in inches.

\(E\) (Modulus of Elasticity):

The modulus of elasticity of the wood species used, in pounds per square inch (psi).

\(I\) (Moment of Inertia):

The area moment of inertia of the beam's cross-section, in inches to the fourth power (in\(^4\)).

Area Moment of Inertia (I)

We calculate the area moment of inertia (\(I\)) of the beam's cross-section using this formula:

Where:

\(I\):Area moment of inertia in inches to the fourth power (in\(^4\)).

\(b\):Actual base width or thickness of the lumber in inches.

\(d\):Actual height of the lumber in inches.

Bending Stress (\(f_b\))

To calculate the actual bending stress, we use this formula:

Where:

\(f_b\):Bending stress in pounds per square inch (psi).

\(M\):Bending moment in pound-force inches (lbf·in).

\(S\):Section modulus in cubic inches (in\(^3\)).

Bending Moment (\(M\))

The bending moment \(M\) is calculated as:

Where:

\(w\):Uniformly distributed load in pound-force per inch (lbf/in).

\(L\):Beam span or unbraced length in inches.

Shear Force (\(V\))

The shear force \(V\) is calculated as:

Shear Stress (\(f_v\))

We calculate the actual shear stress (\(f_v\)) by dividing the shear force by the cross-sectional area of the beam:

Where:

\(f_v\):Shear stress in pounds per square inch (psi).

\(V\):Shear force in pound-force (lbf).

\(A\):Cross-sectional area of the beam in square inches (in\(^2\)).

Wood Species - Modulus of Elasticity (E ×10⁶ psi)

Species	No. 1	No. 2	No. 3	Stud	Const.	Standard	Utility
Alaska Cedar	1.3	1.2	1.1	1.1	1.2	1.1	1.0
Alaska Spruce	1.5	1.4	1.3	1.3	1.3	1.2	1.1
Alaska Yellow Cedar	1.4	1.3	1.2	1.2	1.3	1.1	1.1
Beech-Birch-Hickory	1.6	1.5	1.3	1.3	1.4	1.3	1.2
Coast Sitka Spruce	1.5	1.5	1.4	1.4	1.4	1.3	1.2
Douglas Fir-Larch	1.7	1.6	1.4	1.4	1.5	1.4	1.3
Douglas Fir-Larch (North)	1.8	1.6	1.4	1.4	1.5	1.4	1.3
Douglas Fir-South	1.3	1.2	1.1	1.1	1.2	1.1	1.0
Eastern Hemlock-Balsam Fir	1.1	1.1	0.9	0.9	1.0	0.9	0.8
Eastern White Pine	1.1	1.1	0.9	0.9	1.0	0.9	0.8
Hem-Fir	1.5	1.5	1.3	1.2	1.3	1.2	1.1
Hem-Fir (North)	1.7	1.6	1.4	1.4	1.5	1.4	1.3
Mixed Maple	1.2	1.1	1.0	1.0	1.1	1.0	0.9
Mixed Oak	1.0	0.9	0.8	0.8	0.9	0.8	0.8
Mixed Southern Pine	1.5	1.4	1.2	1.2	1.3	1.2	1.1
Northern Red Oak	1.4	1.3	1.2	1.2	1.2	1.1	1.0
Northern White Cedar	0.7	0.7	0.6	0.6	0.7	0.6	0.6
Norway Spruce (North)	1.3	1.3	1.2	1.2	1.2	1.1	1.1
Red Maple	1.6	1.5	1.3	1.3	1.4	1.3	1.2
Red Oak	1.3	1.2	1.1	1.1	1.2	1.1	1.0
Redwood	1.3	1.2	1.1	0.9	0.9	0.9	0.8
Southern Pine	1.6	1.4	1.3	1.3	1.4	1.2	1.2
Spruce-Pine-Fir	1.4	1.4	1.2	1.2	1.3	1.2	1.1
Spruce-Pine-Fir (South)	1.2	1.1	1.0	1.0	1.0	0.9	0.9
Western Cedars	1.0	1.0	0.9	0.9	0.9	0.8	0.8
White Oak	1.0	0.9	0.8	0.8	0.9	0.8	0.8
Yellow Cedar	1.4	1.4	1.2	1.2	1.3	1.2	1.1